時間の感覚
-楽しい時は短く-
仮説は"時間の一定性を信じる"事から始まる。
皆さん、時間は"楽しいときはすぐ過ぎる"という話をよく聞きますね。
この謎を解く鍵は、またしてもこの男、「アインシュタインの相対性理論」であると言われています。
時間や空間が相対的なものであり、伸びたり、縮んだりするという事らしいです。
筆者は、以前のコンテンツで紹介したように、アインシュタインの相対性理論を否定しています。
(※詳しくは、相対性理論 -アインシュタインの皮肉-を読んで下さい)
筆者は、時間が伸びたり、縮んだりする事を肯定できません。
今回のテーマは「時間が伸び縮みしないのに、どうして楽しい時は短く感じるのか?」です。
導入として、アナログとデジタルの仕組みを説明させて下さい。(分かる人は読まなくていいです。)
アナログとデジタル
まず、普通の数(かず)を考えればイメージ出来るものがアナログです。
1でも、0.1, 0.01, 0.0001, 123, 12.3, 1.23, でも、というように自在に何処をとることも可能です。
一方、デジタルは、例えば1, 2, 3, ... , 10, の数値で考えようと決める訳です。
1.23, 1.2, 1.3 (こういうのは1と考える), 2.23, 2.2, 2.3 (こういうのは2と考える)と決めます。
結果的に1, 2, 3, .... , 10, の数値で全てを考えれます。(これを量子化するといいます。)
さらに、時間経過とともに数値を記録する時には、デジタルデータは時間軸も大雑把にします。
何秒間隔の数値を測定すれば良さそうという感じです。
この間隔で数値を測定してデータをとるのです。(この間隔をサンプリング間隔といいます。)
デジタルデータは大雑把にすればするほど、アナログより情報量が落ちます(軽くなる)。
ここからが本題です。
人間が時を感じる時に何を見ているのでしょうか。
それは、「現在」です。
過去はもうすでに存在しないですね。
筆者は、この感覚を人間は「デジタル」のようにしか感じれていないと仮説を立てました。
何が言いたいかというと、「時間は伸び縮みしない」が、「人間の中でサンプリング間隔が変わる」という事です。
要するに、「楽しい時は、サンプリング間隔が長くなる(時間をあまり気にしない)」というような現象が起きているのではないでしょうか。
人間の感覚は大きさに比例しない
人間の感覚は対数関数的であると言われています。
難しいと感じるかたもいるかも知れないので、比例の関数と対数関数のグラフを書いておきます。
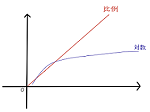
対数関数では、xを大きくしていくと、はじめは極端に大きくなりますが、段々と緩やかになり、変化が少なくなります。
人間の感覚もこの対数関数のようになっており、すごく大きい音はもう少し大きい音と変化が少ないらしいです。
この人間の性質を考えた上で対数関数のグラフに、人間の時間のサンプリング間隔が変動している説を当てはめてみましょう。
サンプリング間隔が短いとは、(1秒当たりの)サンプリングの回数が多いというのと同じ意味です。(測定の頻度が多い)
(1秒当たりの)サンプリングの回数をx軸、時間の感覚をy軸とすると、時間を意識する回数が少ないほど時間が極端に短く感じると言えるでしょう。
時間を意識する頻度をあげていくと、だいたい同じ時間の経過感覚に感じるというわけです。
これは、「筆者の主観」の問題もありますが、実際にそうなっているのではないかと思います。
アインシュタインの相対性理論とは違いますが、この見解も正しく見えるはずです。
最後までご覧いただき、ありがとうございました。